Back to Summary
 
 
 

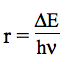
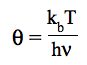
III.3 Description of the Calculation menu
 
 

KiSThelP has been designed to perform statistical mechanics calculations from ab initio quantum chemistry data. This results in the computation of canonical partition functions, molecular thermodynamic properties, thermal equilibrium constants, transition state theory (TST) rate coefficients, and RRKM rate coefficients. One-dimensional tunneling and variational effects have also been incorporated in the TST calculations. It is to be noted that the standard state of pure gaseous species (ideal gas at P0=1 bar) is used in chemical equilibrium and TST kinetic properties computations, but the molecular properties calculated with KiSThelP can also be estimated at any pressure. These properties computations clearly have some limitations the user must be aware of. The Born-Oppenheimer and ideal gas approximations are invoked. The electronic partition function is truncated after the first term. Harmonic oscillator and the rigid-rotor approximation are assumed.

At a given temperature, the data required to derive the vibrational partition functions Qvibv=0 from ab initio calculations are the frequencies (νi) of vibrational modes obtained within the harmonic oscillator approximation. In calculating the vibrational partition function, vibrational energy is measured from the ground state (v=0). But, we also print out QvibBOT obtained by choosing the zero of energy to be the bottom of the potential energy curve. Due to the neglect of anharmonicity in electronic structure computations, it is known that there is a systematic error in the calculated harmonic vibrational frequencies when they are compared to the experimental fundamental vibrational frequencies. A scaling factor is commonly used to correct the calculated value to match the experimental one. KiSThelP gives the possibility to scale harmonic vibrational frequencies by such a factor (directly from the GUI). The harmonic oscillator approximation provides a fast and straightforward method to determine the vibrational frequencies used to compute the partition function of internal modes, but it breaks down for large-amplitude internal motions such as internal rotations. The hindered rotor approximation offers a significant improvement as compared to the harmonic oscillator treatment. That is the reason why the approach of Flagan et al [B. R. McClurg, W. A. Goddard and R. C. Flagan, J. Chem. Phys. 106 (1997) 6675] has been implemented in KiSThelP to account for deviations from the harmonic oscillator (HO) value. The calculations are based on two quantities: θ = kbT/hν and r = ΔE/hν. The deviations proposed by the authors for the vibrational contributions are:

  

     

  

where the corrections ΔU and Q/QHO exclude ZPE contribution and Ix(r/2θ) is the Bessel function of order x. The method used (HRDS) is based on an interpolation scheme between quantum-mechanical partition function at low temperature and the classical partition function at high temperature. The only input parameter to HRDS is the ratio of barrier height to harmonic frequency. However, torsions exhibiting multiple-wells energy curves, with conformers favoured over others conformers cannot be well represented by this method.

Translational partition function, Qtrans, only depends on the molecular mass, temperature and pressure in the ideal gas approximation. For molecules, the moments of inertia derived from the geometry are used as input for calculating the rotational partition function Qrot in the rigid rotor approximation. Three cases are envisaged: single atoms (Qrot is set to 1), linear polyatomic molecules, and general non-linear polyatomic molecules. The rotational symmetry number that compensates for overcounting identical states must be supplied by the user in the input data file. Spacing of electronic energy levels is assumed to be very large compared to kbT so that the excited electronic states do not make a significant contribution to the total partition function. The electronic partition then reduces to the degeneracy of the ground state. The energy of the ground state is set to zero. As usually adopted in statistical mechanics for molecules, vibration, translation, rotation and electronic modes are assumed uncoupled. Hence, in KiSThelP, the partition function of a molecule in its ground state is calculated as: Qtrans × Qrot × Qvib× Qelec. These statistical calculations provide the bridge between quantum mechanics of individual molecules and resulting thermodynamic properties, which are reported in the output. It should be kept in mind that the absolute enthalpies computed from quantum mechanics are relative to infinitely separated electrons and nuclei.
 

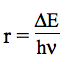
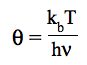
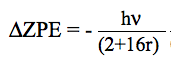
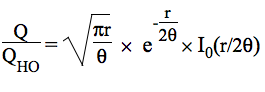
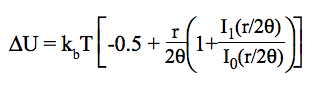
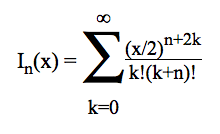
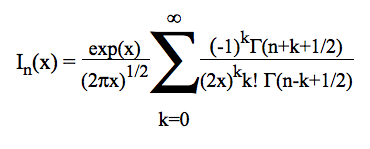
1) Atoms and Molecules :

This menu is to compute statistical and thermodynamical properties of a system (atom or molecule, or TS, or reactionpath point)

KiSThelP can compute these properties :
    - at a single temperature
    - within  a temperature range
    - at a single pressure
    - within a  pressure range

The equations used for computing statistical and thermochemical data in KiSThelP are from standard texts on thermodynamics (see for example [R.A. Alberty and R. J. Silbey, "Physical Chemistry",1st edition, Edited by John Wiley & sons, Inc, ]. Formula employed in KiSThelP are here . The starting point in each case (translational, vibrational, rotational) is the partition function Q(V,T) for the corresponding component of the total partition function.

In addition to the numerical results (statistical and thermodynamical), the Maxwell-Boltzmann distribution (Ni/N) = g(Ei)exp(-Ei/kBT)/Q is plotted as a function of (Ei/kBT). Ei represents energy levels in the translational and ro-vibrational modes. In practice, the degeneracy g(Ei) is evaluated as the product N(Ei) × dEi using the density of states and a small energy grain dEi, respectively. N(Ei) is obtained by convolution using ro_vibrational and translational densities of states (as described by W. Forst [in "Theory of Unimolecular reactions", Academic Press, New York, 1973 and "Unimolecular reactions" , Cambridge University Press,2003]. It also includes electronic degeneracy of the ground state. The density of states of vibrations and rotations have been calculated using the Laplace-transform method, which is based on the inversion of the partition function. For translational modes, a semi-classical approach is employed here, rather than the Laplace-transform method.

KiSThelP is an interactive program that allows the user to change input data directly through the GUI. For single molecular system calculations, the user can interactively test the influence of the mass, potential energy, electronic degeneracy, rotational symetry number, inertia moment, vibrational frequencies, on statistical and thermodynamical properties. The "default values" button restores initial values. Also, a "vibrational" scaling factor field is made available. Default value is 1.0, meaning that no scaling factor is applied. Changing to values ≤ 1 will multiply each initial frequency by this factor.

Similarly, temperature and pressure can be interactively changed from single value to range of values. All the properties are immediately re-computed accounting for new parameters. In the case of a "temperature range" or "pressure range", a 2D-plot is displayed. Selected properties can then be displayed individually. This grahical tools offers several facilities: scales settings, changing titles x/y limits, exporting image (png format), saving numerical data …

An input file must be supplied (.kinp or data fetched from electronic structure calculation results).  

2) k / TST :

        Classical Transition State Theory (TS located at the first-order saddle point)

The method used is the conventional transition state theory [H. Eyring, Chemical Reviews, 17 (1935) 65]. For an overview of TST and its improvements, see also [A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett, and D. G. Truhlar, Chapter 3 in Reviews in Computational Chemistry, 23 (2007) 125 , edited by K. B. Lipkowitz and T. R. Cundari (Wiley-VCH, Hoboken, NJ)].

Conventional TST requires information only for the saddle point and reactant(s). The equation usually presented for the conventional TST is:


where kb is Boltzmann's constant, T is the temperature, h is Planck's constant, NA is Avogadro's number (it disappears for unimolecular reactions rate constants with units of s-1). V‡ is the difference in zero-point excluded potential energy between transition state (TS, assumed to be located at the saddle point on the PES) and reactant(s) (zero point energy contributions are included in the partition functions). QTS and QR denote the total partition functions of the transition state and reactant(s) with the translational partition functions expressed in per unit volume. QTS excludes the reaction coordinate.

The thermodynamic equivalent of the previous equation is employed in KiSThelP:

where ΔG‡,0(T) represents the standard Gibbs free energy of activation for the considered reaction (Δn = 1 or 0 for gas-phase bimolecular or unimolecular reactions, respectively; RT/P0 has the unit of the inverse of a concentration). In the calculation of ΔG‡,0(T), the imaginary frequency that corresponds to the reaction coordinate degree of freedom is removed from the vibrational partition function of transition state, and thus of the kinetic treatment (except for tunneling correction calculation).

        Options :

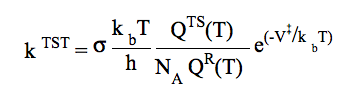
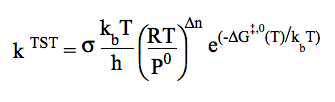
        * UniMolecular Reaction  : to compute an unimolecular rate constant at the Transition State Theory (TST) level
                                                     KiSThelP will ask the user for two data filemanes: one for the reactant, one for the TS (see ReactionPath section)

        * BiMolecular Reaction  : to compute a bimolecular rate constant at the Transition State Theory (TST) level
                                               Reactants data are obtained from separated fragments electronic structure calculations.
                                               KiSThelP will ask the user for three data filemanes: two for the reactant 1 and 2, one for the TS (see ReactionPath section)

   

To determine the reaction path degeneracy σ, thinking about all the various possibilities can rapidly become confusing. Recommended literature are [A. J. Karas, M. A. Collins and R. G. Gilbert, Chem. Phys. Lett. 193 (1992) 181] [A. Fernández-Ramos,B. A. Ellingson, R. Meana-Paneda, J. M. C. Marques and D. G. Truhlar, Theor. Chem. Account 118(2007)813] and [R. G. Gilbert and S. C. Smith, Theory of Unimolecular and Recombination Reactions, Physical Chemistry texts, Blackwell Scientific Publications, 1990] . When calculating reaction rate constants in KiSThelP, it should be noted that the rotational symmetry numbers are removed from all partition functions (reactants, transition state) (even though they must be present in .kinp files) because they are included in the reaction path degeneracy σ. In this case, the user must supply the reaction path degeneracy directly through the GUI. This number is correctly given by: σ= (n‡ × σR)/(nR × σ‡) where n and n‡ are the number of chiral isomers of the reactant(s) and transition state, respectively, and σR and σ‡ are the corresponding rotational symmetry numbers.  

Dual level calculations (combining properties obtained at a low-level of theory with accurate properties computed at a high-level) can be carried out by changing properties values directly in the .kinp files.


KiSThelP can compute rate constants and activation properties:
    - at a single temperature
    - within a temperature range
    - at a single pressure
    - within a pressure range
(it is to be noted that, though the TST rate constant is based on the standard state of pure gaseous species (ideal gas at P0=1 bar), non-standard activation properties can be displayed too).

Temperature and pressure can be interactively changed from single value to range of values. All the properties are immediately re-computed accounting for new parameters. In the case of a "temperature range" or "pressure range", a 2D-plot is displayed. Selected properties can then be displayed individually. This grahical tools offers several facilities: scales settings, changing titles x/y limits, exporting image (png format), saving numerical data …

In addition to all the previous (numerical, graphical) results, the micro-canonical rate constant k(E) in s-1 for an unimolecular reaction is displayed as a function of E/kbT. This involves sum and density of states computations as presented further below in section 8 (RRKM).

KiSThelP also performs two statistical fits to the two- and three-parameters Arrhenius equations : k = Ae -Ea/RT and k = A × Tn e -Ea/RT. In the single temperature mode, teh Arrhenius fit is obtained from a temperature range centred on the selected temperature. In the range temperature mode, the selected range serves to obtain the fit. The corresponding plots are compared to the TST k=f(T) curves. Numerical and graphical results can be saved through the plot tool.


3) k / TST / W :

        Classical Transition State Theory (TS located at the first-order saddle point) including Wigner tunneling correction

One-dimensional quantum mechanical effects on reaction coordinate motion (tunneling and non-classical reflections) are incorporated by a multiplicative transmission coefficient χ(T), so that: kTST/T(T) = χ(T) × kTST(T). In this relative simple treatment, the imaginary frequency (characterizing the reaction mode) is used to compute the Wigner tunneling correction [E. Wigner, Z. Phys. Chem. B, 19 (1932) 203].


       

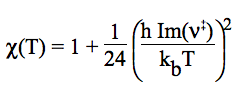
4) k / TST / Eck :

        Classical Transition State Theory (TS located at the first-order saddle point) including Eckart tunneling correction

A Quantum effects in the reaction mode degree of freedom are included by multiplying the TST rate constant by a transmission coefficient. One-dimensional quantum mechanical tunneling treatment through an unsymmetrical Eckart potential energy barrier is involved [C. Eckart, Phys. Rev. 35 (1930) 1303 ]. This methodology requires no ab initio calculations at points other than reactants, products, and saddle point. User will be asked for the ZPE corrected reverse energy barrier. The tunneling effect is accounted for by a multiplicative factor, so that: kTST/T(T) = χ(T) × kTST(T).

The analytic form proposed by Eckart can model a variety of physically reasonable shapes (involving unsymmetrical forms) and admits an analytical solution of the corresponding Schrödinger equation and then for the probability p(E) of transmission through the corresponding 1-D barrier at energy E. Original formula are used in KiSThelP with L, the width of the transition region which can be defined in term of the imaginary frequency ν‡ characterizing the reaction mode (that is routinely obtained from electronic structure calculations).




The two constants (A,B) determining the overall shape of the Eckart barrier are directly linked to the zero-point-corrected energy barriers in the reverse and forward direction computed by KiSThelP: ΔH‡,0r and ΔH‡,0f See [ "Unimolecular reactions" , Cambridge University Press,2003] for more details. Finally, the Eckart tunnelling correction χ(T) is obtained by numerically integrating p(E) over a Boltzmann distribution of energies.

In KiSThelP, the algorithm uses a 15-point Gauss-Laguerre integration. In the case of an endothermic reaction, roots of 15th degree Laguerre polynomial are distributed on an energy range above A. The Gauss-Laguerre scheme can still be used by means of an integration variable change, leading to:



However, the potential energy along IRC has not always a shape such that the tunneling probability cannot be usefully approximated by an Eckart potential. Furthermore, although convenient to carry out,and thus attractive, these methods (Wigner and Eckart) do not take into account the full dimensionality of the quantum effect. One of the possible extensions of KiSThelP is to program the semi-classical WKB approximation in order to better estimate the permeability P(E), using zero curvature tunneling (ZCT, which does not include corner-cutting tunneling) or event more accurate small-curvature tunneling (SCT) or large curvature tunneling (LCT) approaches. See [A. Fernandez-Ramos, B. A. Ellingson, B. C. Garrett, and D. G. Truhlar, Variational Transition State Theory with Multidimensional Tunneling Chapter 3 in Reviews in Computational Chemistry, 23 (2007) 125 , edited by K. B. Lipkowitz and T. R. Cundari (Wiley-VCH, Hoboken, NJ)] for a more detail discussion about these approaches.

       

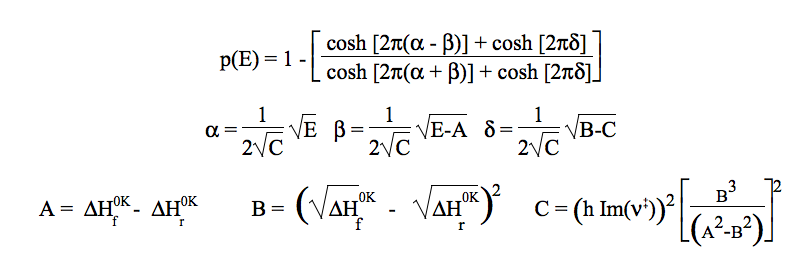
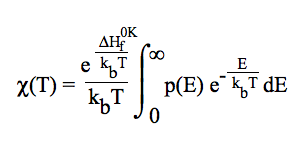
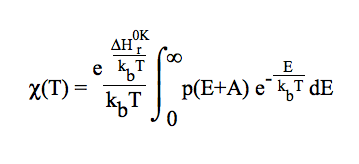
5) k / VTST :
 

       Generalized Transition State Theory (TS located variationally; the optimum TS corresponds to a maximum free energy of activation at a given temperature) 


Available in KiSThelP, the variational transition state theory (CVT) involves a generalized transition state rate constant:


where s is the distance along the minimum energy reaction path (MEP) in isoinertial coordinates. In this theory (CVT), the rate constant kCVT(T) is obtained by minimizing kGT with respect to s along the reaction path. The thermodynamic equivalent of the previous equation is employed in KiSThelP (kCVT(T) is obtained by minimizing the generalized free energy of activation ΔG‡,0(T)GT). In this case, addition information is needed on the PES. The MEP can be obtained by performing a so-called intrinsic reaction path (IRC) calculation using a quantum chemistry software. By convention, s=0 at transition state structure, s <0 on reactant side and s> 0 on product size.

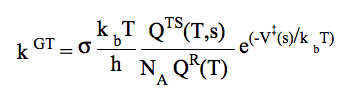
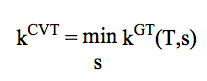
In VTST, the required information is the Minimum Energy Path (MEP) information obtained from electronic structure calculations. This information is read from a raectionpath .kinp input file containing as "POINT" sections as points calculated along the reaction path (including the transition state). The coordinate reaction, potential energy, inertia moment, ... (see ReactionPath section) must be supplied for each point.

Remarks: 

- As abovementioned for conventional TST, the reaction path multiplicity is given by the user through KiSThelP graphical interface

- Along the reaction path, ideally, all bound modes transverse to the reaction path should be characterized by no imaginary frequency in KiSThelP. But practically, from electronic structure calculations, a reactionpath point can have 0, 1, or more than one imaginary boundary modes normal to the reaction mode. In KiSThelP, 0 or 1, or more imaginary frequencies will be accepted for a reaction path point. But if 0 imaginary frequency is found, then, to handle a homogeneous set of data the smallest frequency is set to imaginary number to design the reaction mode (thus it is removed from statistical and kinetics treatments). If more than 1 imaginary frequency are found, corresponding imaginary frequencies are removed from statistical treatments. In all these cases, warnings will be delivered to the user.

6) k / VTST / W :
 

       Generalized Transition State Theory (TS located variationally; the optimum TS corresponds to a maximum free energy of activation at a given temperature)  including Wigner tunneling correction

To include quantum effects on reaction coordinate motion the rate constant kCVT(T) is multiplied by a transmission coefficient χ(T): kCVT/T(T) = χ(T) × kCVT(T). The imaginary frequency of the transition state (1-order saddle point on the potential energy surface) is used to compute the Wigner tunneling correction.

7) k / VTST / Eck :

    Generalized Transition State Theory (TS located variationally; the optimum TS corresponds to a maximum free energy of activation at a given temperature)  including Eckart tunneling correction

The tunneling effect is accounted for by a multiplicative factor, so that: kCVT/T(T) = χ(T) × kCVT(T). A one-dimensional quantum mechanical tunneling treatment through an unsymmetrical Eckart potential energy barrier is involved. This methodology requires no ab initio calculations at points other than reactants, products, and saddle point. User will be asked for the ZPE corrected reverse energy barrier.

8) RRKM:

    Treatment of unimolecular processus in gas phase. Transition state theory reformulated on a microcanonical basis. Pressure effects can be accounted for.


The implementation of this method in KiSThelP is based on the following books: (1)[K.A. Holbrook, M.J. Pilling and S. H. Robertson, "Unimolecular Reactions", Wiley & sons Eds, 1996] (2)[P. J. Robinson and K.A. Holbrook,"Unimolecular Reactions" Wiley-Interscience, London, 1972], [W. Forst, "Unimolecular reactions" , Cambridge University Press,2003]. Only reaction paths with a well defined 1st-order saddle point on the potential energy surface are considered here (Tight TS). The other cases (Loose transition state) represent one of the perpectives for futur developpments of KiSThelP.

        * TightTS : to compute an unimolecular rate constant using the RRKM theory within the rigid TS model

- KiSThelP will ask the user for two data filemanes: one for the reactant, one for the TS (see ReactionPath section)

- Next, KiSThelP will ask for molecular mass (diluent gas), ε/kb (in K) and σ(cm) for reactant and diluent gas respectively. These data will serve to estimate the deactivation rate constant within the RRKM unimolecular kinectic mechanism. Data may be found using the KiSThelP "Data/Lennard-Jones parameters" menu

- The user can then interactively test the influence of the statistical factor, collision efficiency and critical energy E0 values, on the unimolecular rate constant, through the GUI.

- KiSThelP can compute the rate constant:

- at a single temperature
- within a temperature range<
- at a single pressure
- within a pressure range
 

        (* LooseTS : not implemented in this version)



The thermal rate constants of the unimolecular reactions are obtained by applying the RRKM theory to predict the falloff behaviour. The microcanonical rate constants k(E) are calculated by the standard RRKM expression:



where σ is the reaction path degeneracy, G(E) is the total number of states of the transition state with energy less than or equal to E, and N(E) is the density of states of the dissociating reactant species. Reactant and transition state are approximated as symmetric tops and the external K-rotor, associated with the smallest moment of inertia, is treated as an active degree of freedom completely coupled to the vibrations. Laplace-transform method based on the inversion of the partition functions is employed for the calculation of the sum of states G(E) and density of states N(E). The thermal rate constant is obtained by using the following expression:

where σ is the reaction path degeneracy, h is the Planck's constant, Q2 is the partition function of the active degrees of freedom (vibrations + K-rotor) of the reactant, Q‡1 and Q1 are the partition functions for adiabatic rotations of the transition state and of the reactant, respectively, E0 is the zero-point-corrected threshold energy. The strong collision approximation is used assuming that every collision deactivates with ω=βcZLJ[M] being the effective collision frequency where βc is the collisional efficiency, ZLJ is the Lennard-Jones collision frequency and [M] is the total gas concentration. ZLJ are calculated using the Lennard-Jones parameters: ε/kb (K) and σ (cm) according to the equations (3.1) and (3.3) from reference [J. Troe, J. Chem. Phys. 66, 4758 (1977); doi: 10.1063/1.433838 ]. Such parameters may be found using the KiSThelP "Data/Lennard-Jones parameters" menu. In order to account for the centrifugal effect in the rate constant calculation, the factor Q‡1/Q1 was included in the expression of k(T) and k(E) is evaluated at the energy E including <ΔEj> with <ΔEj> = (1- I‡/I)× kbT where I‡ and I are the average of the two largest moments of inertia. It accounts for the release (or uptake) of a certain amount of the rotational energy associated with the external two-dimensional inactive rotation (J) into the active degrees of freedom as the system approach the transition state. The thermal rate constant is obtained using a 15-point Gauss-Laguerre integration. For the 15 roots of the Laguerre polynomial numerical values of G(E), N(E) and k(E) are given. In addition, the k(E) plot is displayed for energy values up to 100 kbT. Low- and high-pressure limits (k0 and k∞) are also given. Neither variational theory nor tunneling effect have been implemented in the present version of KiSThelP. This is one of the perspectives for futur KiSThelP developments.


9) Keq :

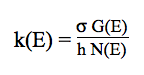
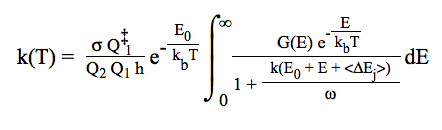
    Calculation of gas-phase chemical reaction equilibrium constants

The knowledge of equilibrium constants is important in the study of chemical reaction mechanisms. In addition to allowing the prediction of the composition of a mixture, the equilibrium constant is also connected to rate constants through the existence of equilibrium between stable species in multiplestep processes. Furthermore, in simulations of gas-phase mixtures, backward rate can be found using the forward rate and the equilibrium constant. In other respects, the equilibrium constant is a practical indicator to test theoretical methods because it is very sensitive both to the energy quality and to geometrical parameters and also because the electronic structure of each compound that takes part in the equilibrium is extremely different from the others.

To compute an equilibrium constant betwen reactant(s) and product(s)for a given balanced equation,stoichiometric coefficients must be supplied. The thermodynamical expression of the equilibrium constant for gas-phase reactions is employed in KiSThelP:


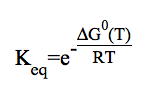
where ΔG0(T) is the change in standard Gibbs energy. The standard state of a pure gaseous substance is used (ideal gas at one bar pressure). It is to be noted that non-standard reaction properties (ΔH;, ΔS, ΔG) can be displayed too. Reactants data are obtained from separated electronic structure calculations. KiSThelP will ask the user for the number of reactants and products in the studied balanced equation. For each species, one data filename and stoechiometric coefficient must be provided. (see Reactant (or Product) section)
 

KiSThelP can compute gas-phase equilibrium constants :
    - at a single Temperature
    - within  a temperature range
 

10) Reset :

  This menu will reset the current calculation.
 

Back to Summary